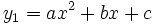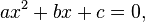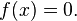TUJUAN PENDIDIKAN INKAI
Mendidik manusia Indonesia seutuhnya dengan cirri-ciri sebagai berikut:
Berkepribadian luhur
Berbudi pekerti yang luhur
Memiliki daya juang yang tinggi
Menjunjung nilai-nilai etika
Memiliki kedewasaan mental melalui Karate-Do
SUMPAH KARATE
Sanggup memelihara kepribadian
Sanggup patuh pada kejujuran
Sanggup mempertinggi prestasi
Sanggup menjaga sopan santun
Sanggup menguasai diri

ARTI LAMBANG DAN WARNA

Bulatan Bumi berwarna Merah dan Putih yang diikat Sabuk Hitam di dalam sebuiah lingkaran dengan warna dasar Kuning, melambangkan anggota INKAI yang bersatu padu dalam satu ikatan kekeluargaan berdasarkan prinsip-prisip Karate-Do.
MERAH melambangkan keberanian
PUTIH melambangkan suci
HITAM melambangkan keteguhan tekad dan percaya pada diri sendiri
KUNING melambangkan keanggunan kepribadian
Sejarah Perkembangan Karate di Indonesia
Di Indonesia karate dikenal sejak kembalinya mahasiswa Indonesia yang belajar di Jepang. Bersamaan, beberapa orang mereka memperkenalkan dan mendirikan semacam perkumpulan olahraga karate di Indonesia. Beberapa tokoh pendiri antara lain: R. Baud Adikusumo, H. Moctar MR (pemegang sabuk hitam pertama di Indonesia), Albert Lumban Tobing, Ottoman Noeh dan lain-lain. Pada akhirnya berdirilah Persatuan Olagraga Karate Indonesia (PORKI). Pada tahun 1968 berdatang lagi mahasiswa-mahasiswa yang belajar di Jepang, meramaikan perkaratean di Indonesia diantaranya A.C Suwarto, Anton Lesiangi, Sabeth Mucshin, Wono Sarono, Koes Pratomo dan lain-lain.
Namun sayangnya pada kongres ke III PORKI pada tahun 1970, timbul perpecahan ditubuh PORKI yang pada akhirnya aliran Shotokan di Indonesia pecah menjadi tiga perguruan yaitu INKAI, INKADO, LEMKARI, sebagai gantinya PORKI berubah menjadi FORKI (Federasi Olahraga Karate-Do Indonesia).
Sejarah Berdirinya INKAI
Pada tanggal 15 April 1971, di Jakarta, beberapa karateka aliran Shotokan mendirikan suatu perguruan dengan nama Institut Karateka-Do Indonesia (INKAI) dengan ketua umumnya pertamanya Letjen TNI G.H. Mantik dan sebagai ketua dewan guru Drs. Sabeth Mucshin dengan anggota Wono Sarono, Ottoman Noeh, A. Latief, Dr Nico A. Lumenta, Albert Lumban Tobing dan A.S.J. Siregar.
Tanggal 25 Mei 1971, INKAI resmi berdiri sebagaiperguruan anggota FORKI dan oleh PB FORKI, INKAIditunjuk mewakili Indonesia mengikuti kejuaraan karate WUKO 1 di Jepang. Dan INKAI juga merupakan anggota resmi affiliasi JKA yang berkedudukan di Jepang.

BY http://inkaijusufk.blogspot.com/

RUMUS FUNGSI KUADRAT

Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah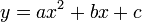

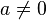
dengan

Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari x², koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.

arti nilai a, b, dan c

Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.

• a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a <> akan menyebabkan parabola terbuka ke bawah.
• b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
• c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.
• 
  

• Rumus kuadrat akar rumus abc

  Rumus kuadrat dikenal pula dengan nama ‘rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b danc suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk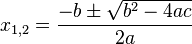
  
  
  
  Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa
  
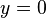  Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk
  
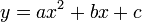  dapat dituliskan menjadi
  
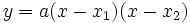  Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu
  
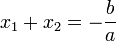  dan
  
  
  
  
  

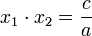
  Diskriminan/determinan

  Akar-akar dan nilai D.

  Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:

  

  yang disebut sebagai diskriminan atau juga sering disebut determinan suatu persamaan kuadrat. Kadang dituliskan sebagai D.

  
  

  Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:

  
  

  • Jika dikriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional — sebaliknya dapat pula merupakan bilangan irrasional kuadrat.

  • Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:
  • 
  • Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
  • dan
  • Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilaitidak negatif.
  • 
    

  • Akar riil dan kompleks

    Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagaititik potongnya dengan sumbu x atau garis y = 0.
    
    

    Titik potong dengan garis y = d

    
    

    Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat

    • • 

    dengan suatu garis mendatar

    • • 
    Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.
  • 

  • Intepretasi yang sama pun berlaku, yaitu bila:

    • diskriminan positif, terdapat dua titik potong antara dan ,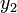
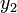    • diskriminan nol, terdapat hanya satu titik potong antara dan , dan
    • diskriminan negatif, tidak terdapat titik potong antara kedua kurva, dan .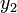

    • Nilai-nilai y

      Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai yberharga positif atau negatif. Harga-harga ini ditentukan pula oleh nilai konstanta kuadrat a:

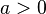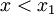
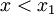
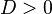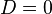
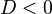
      Harga-harga y 0\!"> x_2\!"> x_2\!"> 0\!"> 0\!"> 0\!"> 0\!"> 0\!"> 0\!"> 0\!">
      0\!">
      
      

  • 
    

  dengan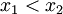 merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila 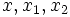bersifat kompleks, maka yang dimaksud adalah 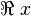(nilai riil)-nya.

  
  

  Geometry

  Untuk fungsi kuadrat:
  f(x) = x² − x − 2 = (x + 1)(x − 2), dengan variabel x adalahbilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akardari persamaan kuadrat : x² − x− 2 = 0.

  Akar-akar dari persamaan kuadrat

  

  adalah juga pembuat nol dari fungsi kuadrat tersebut:

  

  dikarenakan akar-akar tersebut merupakan nilai yang memberikan

  

  Jika a, b, dan c adalah bilangan riil, dan domain dari 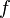adalah himpunan bilangan riil, maka pembuat nol dari 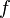adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.

  Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurvapersamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.

  
  

  
  

  by

  • http://dana160.student.umm.ac.id/2010/02/05/rumus-fungsi-kuadrat/