Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah 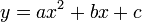
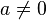
arti nilai a, b, dan c
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.
- a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a <> akan menyebabkan parabola terbuka ke bawah.
- b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
- c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.
-
Rumus kuadrat akar rumus abc
Rumus kuadrat dikenal pula dengan nama ‘rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b danc suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk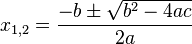 Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa
Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa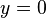 Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk
Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk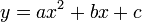 dapat dituliskan menjadi
dapat dituliskan menjadi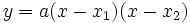 Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu
Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu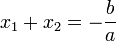 dan
dan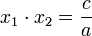
Diskriminan/determinan
Akar-akar dan nilai D.Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar: yang disebut sebagai diskriminan atau juga sering disebut determinan suatu persamaan kuadrat. Kadang dituliskan sebagai D.Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:
yang disebut sebagai diskriminan atau juga sering disebut determinan suatu persamaan kuadrat. Kadang dituliskan sebagai D.Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini dikriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:- Jika dikriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional — sebaliknya dapat pula merupakan bilangan irrasional kuadrat.
- Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah:

- Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:
 dan
dan 
- Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilaitidak negatif.
-
Akar riil dan kompleks
Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagaititik potongnya dengan sumbu x atau garis y = 0.Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.Titik potong dengan garis y = d
Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadratdengan suatu garis mendatar
Intepretasi yang sama pun berlaku, yaitu bila:
- diskriminan positif, terdapat dua titik potong antara
 dan
dan 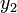 ,
, - diskriminan nol, terdapat hanya satu titik potong antara
 dan
dan 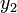 , dan
, dan - diskriminan negatif, tidak terdapat titik potong antara kedua kurva,
 dan
dan 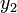 .
. Nilai-nilai y
Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai yberharga positif atau negatif. Harga-harga ini ditentukan pula oleh nilai konstanta kuadrat a:
Harga-harga y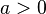 0\!">
0\!">
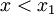

 x_2\!">
x_2\!">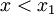

 x_2\!">
x_2\!">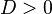 0\!">
0\!"> 0\!">
0\!">
 0\!">
0\!">
 0\!">
0\!">
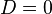
 0\!">
0\!">
 0\!">
0\!">


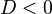
 0\!">
0\!">
 0\!">
0\!">


- diskriminan positif, terdapat dua titik potong antara
-
dengan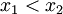 merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila
merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila 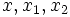 bersifat kompleks, maka yang dimaksud adalah
bersifat kompleks, maka yang dimaksud adalah 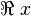 (nilai riil)-nya.
(nilai riil)-nya.Geometry
Untuk fungsi kuadrat:
f(x) = x2 − x − 2 = (x + 1)(x − 2), dengan variabel x adalahbilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akardari persamaan kuadrat : x2 − x− 2 = 0.Akar-akar dari persamaan kuadrat
adalah juga pembuat nol dari fungsi kuadrat tersebut:
dikarenakan akar-akar tersebut merupakan nilai
 yang memberikan
yang memberikanJika a, b, dan c adalah bilangan riil, dan domain dari
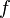 adalah himpunan bilangan riil, maka pembuat nol dari
adalah himpunan bilangan riil, maka pembuat nol dari 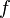 adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.
adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurvapersamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.

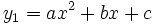

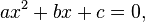

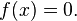
Selamat datang di S128Cash Agen Betting Judi Online Teraman dan Terpercaya.
BalasHapusKini kami hadir untuk Anda semua dengan memberikan berbagai macam PROMO BONUS, seperti :
- BONUS NEW MEMBER 10%
- BONUS DEPOSIT SETIAP HARI 5%
- BONUS CASHBACK 10%
- BONUS 7x KEMENANGAN BERUNTUN !!
Sudah pastinya juga kami menyediakan permainan Terbaik yang digemari para Bettor, yaitu Sportsbook, Live Casino, Sabung Ayam Online, IDN Poker dan masih banyak permainan lainnya.
Hanya dengan bermodal Rp 25.000,- Anda sudah bisa menikmati semua permainan yang tersebut.
Jadi apa lagi yang Anda tunggu? Segera daftarkan diri Anda bersama kami !!
Hubungi kami :
- Livechat : Live Chat Judi Online
- WhatsApp : 081910053031
Link Alternatif :
- http://www.s128cash.biz
Judi Bola
Rumus Judi Bola Over Under